DÉTONIQUE

DÉTONIQUE

La détonique est apparue dans la seconde moitié du XIX^e siècle, bien avant le terme qui la désigne. Sa naissance est due à la conjonction des premières synthèses de molécules explosives et de la théorie des ondes de choc en milieu condensé.

Actuellement, lorsqu’un missile perce le blindage d’un char, lorsqu’une explosion souterraine est détectée ou lorsqu’une route de montagne est ouverte, ces divers événements ont à leur source un même phénomène: la détonation d’un explosif. Celle-ci est la manifestation de la propagation très rapide d’une onde réactive dont les deux composantes, une onde de choc et une réaction chimique, s’entretiennent mutuellement pour libérer une importante énergie en un temps extrêmement bref. En termes de production, si les besoins civils en explosifs excèdent de beaucoup les besoins militaires, les recherches sur lesquelles repose la détonique actuelle ont, comme souvent, leur origine dans ces derniers.

La détonique avait atteint, en quelque sorte, l’«âge de raison» avant la Première Guerre mondiale, puisque le modèle de détonation encore aujourd’hui le plus couramment employé était déjà élaboré. Mais l’entrée de la détonique dans l’âge adulte coïncide avec le projet Manhattan et le fonctionnement de la première arme nucléaire.

En tant que discipline, elle s’est depuis lors enrichie des apports d’une instrumentation de plus en plus sophistiquée et du développement des moyens informatiques scientifiques. Désormais, celle-ci englobe le domaine des détonations et celui des applications au fonctionnement des têtes explosives.

1. Une discipline jeune d’un siècle

De nombreuses substances solides, liquides ou gazeuses peuvent être le siège d’une détonation. Pour l’utilisateur, les explosifs condensés, qui recèlent l’énergie maximale sous un volume donné, sont les plus intéressants. La poudre noire, dont le seul régime de décomposition attesté est la déflagration, est demeurée l’unique substance explosive disponible jusqu’au milieu du XIX^e siècle. À cette époque, la découverte de la nitroglycérine, la reconnaissance du caractère explosif de nouvelles molécules (mélinite, tolite..) ont ouvert la voie aux études sur la détonation en milieu condensé.

De fait, les explosions chimiques, qui dégagent en un temps extrêmement bref un grand volume de gaz, se répartissent en déflagrations et détonations. Pour que ces phénomènes se produisent au sein d’une substance chimiquement stable, il est nécessaire de communiquer à celle-ci, localement et rapidement, une énergie d’activation suffisante. Les couches adjacentes réagiront de proche en proche si une telle énergie leur est transmise. Une réaction auto-entretenue ne se propagera donc que si la décomposition est suffisamment exothermique. En général, le mode de transfert de l’énergie sera thermique ou mécanique.

Les premiers jalons de la détonique ont été posés vers la fin du XIX^e siècle. En observant qu’un transfert principalement thermique était la cause d’une célérité de propagation de quelques centaines de mètres par seconde, Paul Vieille caractérisait ainsi les déflagrations. Une célérité d’un ordre de grandeur supérieur, spécifique des détonations, ne pouvant résulter que d’un transfert mécanique par onde de choc, il établissait ainsi le lien avec les travaux contemporains d’Henri Hugoniot en ce domaine.

Par la suite, des considérations de sonicité dans l’écoulement réactif ont conduit à imaginer un couplage strict entre l’onde de choc et la réaction chimique, et à postuler l’existence de régimes permanents de détonation. L’élaboration du schéma de David Leonard Chapman et Émile Jouguet au début de ce siècle en résulte. Il comporte une zone de réaction stationnaire dans sa propagation, qui maintient en amont un front de choc d’intensité constante et engendre en aval une détente à partir de conditions également stationnaires (fig. 1 a).

Depuis lors, ce schéma est resté le plus utilisé, bien que divers auteurs, tel Roger Chéret en France, aient développé des formalismes plus élaborés. En vérité, l’essor considérable de la détonique qui s’est manifesté à partir de la Seconde Guerre mondiale s’explique par un besoin majeur (les armes nucléaires) et une évolution fantastique des moyens (métrologie spécifique et simulation numérique).

2. Caractéristiques de détonation des explosifs

L’onde de détonation idéale

Compte tenu de leur brièveté et de leur violence, la répétitivité et la reproductibilité des phénomènes observés ont constitué une grande chance pour les premiers «détoniciens», qui ne disposaient que d’une instrumentation sommaire. Cela a en effet puissamment simplifié leur tâche dans l’élaboration, puis la confirmation du modèle de la détonation idéale, qui est, par définition, monodimensionnelle, plane et se propage en régime permanent dans un milieu illimité.

Une telle onde (fig. 1a) présente une célérité constante D par rapport à l’explosif au repos. La «zone de réaction», siège des réactions irréversibles, y est d’épaisseur fixée. Elle s’étend du front de détonation au plan dit de Chapman-Jouguet (plan C.J.), où les produits de détonation parvenus à l’équilibre chimique ont acquis une vitesse matérielle u . Les grandeurs caractéristiques y sont la pression, le volume spécifique, la température, l’énergie interne spécifique, la célérité du son (P , V , T , E , a ).

Une détonation idéale est caractérisée par l’état de Chapman-Jouguet de l’explosif, soit la composition des produits de réaction et les conditions thermodynamiques et cinématiques qui y règnent. Le problème, de nature à la fois chimique et mécanique, a pour pierre angulaire l’équation d’état du milieu. Sa connaissance est indispensable au tracé de la surface d’état sur laquelle est particularisé le point représentatif de l’état C.J., puis à la détermination de la valeur des constantes des équilibres qui s’y manifestent.

Approche mécanique et chimique des détonations idéales

L’écriture des trois lois de conservation de la mécanique (masse, impulsion, énergie) entre l’état initial et l’état C.J. conduit, après combinaison, aux trois relations:

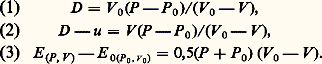La figure 1 b représente le diagramme pression-volume spécifique, l’état initial de l’explosif (point A), l’état final atteint par un choc réactif stationnaire (courbe de Crussard, C), l’état final d’un choc non réactif stationnaire (courbe d’Hugoniot, H) et des droites (dites de Rayleigh) issues de A et dont la pente caractérise directement la célérité de l’onde en relation avec l’équation (1).

Pour une célérité d’onde donnée et en régime permanent, l’état dans un plan situé à une distance fixe du front d’onde est représenté par un point fixe de la droite de Rayleigh. Il y a au plus deux points B¹ et B² qui caractérisent l’état final sur C. Ce fut l’apport de Chapman et Jouguet d’avoir montré que seul le point I convenait à un régime permanent. La célérité de détonation y est minimale et la droite de Rayleigh tangente à la courbe de Crussard et à l’isentropique locale, d’où une relation dont la forme la plus usitée est:

Elle permet, en association avec (1), (2) et (3), d’obtenir D , u , P et V . Par ailleurs, le point VN est attaché au front de détonation. Son ordonnée, qui excède largement la pression de Chapman-Jouguet, constitue le pic de von Neumann.

Exception faite de certaines formules contenant un métal ou un halogène, l’aspect chimique des détonations implique le plus souvent des compositions à base de carbone, d’hydrogène, d’oxygène et d’azote. Des très nombreuses espèces recombinées après la réaction de décomposition, on ne retient souvent que celles de concentration significative: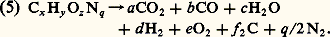

La composition des produits de détonation se calcule en ajoutant aux trois équations de conservation des atomes (C, H, O) la loi d’action de masse relative à trois équilibres chimiques indépendants entre espèces formées à l’état C.J. Pour une formule initiale et des constantes d’équilibre données, un excès d’oxygène ou d’atomes réducteurs peut apparaître. Un «bilan d’oxygène» équilibré constitue la situation optimale au plan énergétique.

Caractéristiques générales des détonations

Sur ces bases, il existe de nombreux logiciels qui calculent avec une grande précision l’état C.J. des explosifs. Diverses approximations sont également utilisées. L’une d’elles, particulièrement simple et connue, est l’approximation polytropique. Elle postule que, au voisinage de l’état C.J., l’équation d’état des gaz parfaits convient pour représenter les produits de détonation. Cela est bien vérifié si l’on admet pour l’exposant de la relation isentropique une valeur très éloignée des cas usuels (voisine de trois). La célérité du son s’exprime alors simplement dans la relation (4) et le système (1), (2), (3), (4) devient aisément soluble.

Les conclusions qui en résultent, appliquées à un explosif de densité 1,8 et de célérité de détonation égale à 8 500 m/s, en pratique très performant, sont les suivantes:

– la matière acquiert, dans le sens de propagation de l’onde, une vitesse excédant 2 000 m/s;

– la pression initialisant la détente dépasse 32 GPa;

– la densification du milieu est voisine de 33 p. 100.

Ces paramètres varient suivant les explosifs (cf. tableau). La densité est un facteur majeur de performance. Sous l’angle de la composition, la forte carbonation de la tolite et du tétryl leur est préjudiciable; la pentrite et la nitroglycérine bénéficient de leur bonne oxygénation. Une forte densité et un bilan d’oxygène assez équilibré font de l’hexogène et de l’octogène des explosifs très performants. Ces constats sont conformes aux règles édictées par M. J. Kamlet, selon qui le fait de limiter la phase condensée et de réduire la masse moléculaire des produits de détonation augmente les performances des compositions.

3. Régimes de détonation non idéaux

Par rapport à l’onde idéale, les régimes observés dans la réalité sont transitoires ou permanents non idéaux. Ainsi (fig. 2), après un premier régime transitoire d’amorçage d’une zone limitée d’explosif, une onde stationnaire s’établit si les conditions géométriques le permettent. Leur modification crée ensuite un nouveau régime transitoire.

Détonation stationnaire d’une cartouche cylindrique

Après une phase sphérique divergente résultant d’un amorçage au centre d’une de ses extrémités, la détonation d’une cartouche cylindrique évolue vers un régime permanent. Selon M. A. Cook, cela se produit lorsque la détonation a parcouru trois fois le diamètre de la cartouche. Les effets de bord associés à la limitation latérale de l’explosif rendent ce paramètre dominant. Ils se manifestent en effet dès le passage du front de détonation et affectent la zone de réaction.

Une chute rapide de la pression à la périphérie de la cartouche altère la réactivité de l’explosif, réduit la célérité de l’onde et impose une courbure permanente du front de détonation. Ces phénomènes augmentent si le diamètre diminue. En deçà d’une certaine valeur, appelée diamètre critique, une détonation permanente ne peut s’établir ou se maintenir. Cette caractéristique essentielle pour l’emploi des explosifs est très variable suivant celui qu’on utilise. Inférieure au millimètre pour la pentrite, cette valeur atteint une fraction de centimètre pour les compositions militaires usuelles et excède couramment cette dernière pour des explosifs à usage industriel.

De nombreux auteurs (H. Jones, H. Eyring...) ont tenté de modéliser l’influence du diamètre sur la célérité de l’onde. Une généralisation de la relation correspondante a été tentée par Berger et Viard lorsqu’un confinement inerte limite les détentes latérales. Le plus souvent, la célérité de détonation croît linéairement avec l’inverse du diamètre. L’intérêt de cette observation est de livrer, par extrapolation de la droite représentative, la célérité de Chapman-Jouguet des explosifs, qui en est l’ordonnée à l’origine.

Régimes transitoires de détonation

Si la configuration cylindrique sert surtout à la caractérisation intrinsèque des explosifs, leur détonation s’effectue en pratique selon des régimes transitoires. Consécutifs à un amorçage localisé ou à l’organisation (fréquemment à symétrie de révolution) des édifices explosifs, ils sont sous l’influence directe des frontières du milieu.

L’énergie d’amorçage d’un explosif est amenée par des moyens appropriés (détonateur, impact...) à sa périphérie en un point, une ligne ou une aire donné. Selon le moyen considéré, les conditions minimales d’établissement d’une détonation constituent la sensibilité de la substance. À partir de ce seuil, la notion d’amorçabilité fait en outre intervenir la distance et le délai requis pour obtenir cette détonation. La nature chimique et la texture de la composition, fixant la cinétique de décomposition et l’énergie d’activation et en régissant le dépôt, sont les principaux paramètres influents. Ainsi, la pentrite se révèle plus sensible ou amorçable que la tolite. Il en est de même de la pentrite pulvérulente vis-à-vis de la pentrite compacte.

Une augmentation brusque du diamètre affecte peu l’onde stationnaire, instant t ², dans sa propagation axiale, instant t ³ (fig. 2). Son expansion radiale est commandée par la pression régnant à la périphérie du front d’onde. Pour un diamètre initial limité, l’établissement d’une détonation franche peut être difficile. Si l’amorçabilité de l’explosif est faible, une zone torique proche de la surface libre peut même ne pas réagir. C’est pourquoi cette configuration est d’un grand intérêt pour l’étude de la propagation non rectiligne des détonations.

4. Emploi balistique des explosifs

Les effets induits par une détonation dans les milieux connexes aux explosifs sont divers (effet de souffle, explosion sous-marine...). Un cas fréquent est la propulsion à grande vitesse de matériaux de revêtement minces formant des projectiles. La maîtrise des modalités de conversion de l’énergie chimique des explosifs en énergie cinétique des revêtements est étudiée à cette fin.

Transfert d’énergie

L’action d’un explosif en détonation sur un revêtement peut se produire de maintes façons. Les configurations simplifiées (fig. 3) en permettent une étude fine. Le revêtement latéral est relevé d’abord par le choc induit, puis par la poussée des produits de détonation. L’onde étant stationnaire, la mise en vitesse du revêtement l’est également. La valeur finale atteinte donne accès au «rendement de transfert d’énergie» de l’explosif, au moyen de formules dont la plus ancienne est due à R. W. Gurney. L’expérience montre que la part du choc induit dans ce rendement est très minoritaire.

Si l’échantillon est parallélépipédique et confiné sur une face, une relation linéaire, établie par H. Richter, lie l’inverse de l’angle de relèvement au rapport des masses de revêtement et d’explosif en regard. Observant qu’il existe alors une valeur de ce rapport pour laquelle l’énergie cinétique du revêtement par unité de masse d’explosif est maximale, M. Defourneaux en a tiré une méthode de classification des compositions couramment utilisée en France, selon cette énergie maximale appelée «capacité balistique».

En géométrie de révolution, la mesure fine de la mise en vitesse du revêtement a permis à une équipe de Livermore en Californie (L.L.N.L.) d’accéder à l’équation d’état des produits de détonation. La poussée qu’ils exercent lors de leur détente sur un confinement dépend directement de cette équation. Avec une forme empirique traitant implicitement l’évolution chimique du milieu, il est possible de restituer les résultats expérimentaux à l’aide d’un logiciel de calcul, par approximations successives sur la valeur des paramètres de calage de l’équation d’état. Le résultat obtenu permet la simulation numérique ultérieure de cas plus complexes.

Fonctionnement des charges formées

Les considérations précédentes trouvent une application majeure dans les armes nucléaires, pour la mise en condition des matériaux fissiles. Depuis les années soixante, elles interviennent de plus en plus dans l’optimisation des munitions classiques, et tout particulièrement des charges formées. Étant à symétrie de révolution, elles présentent un évidement axial tapissé d’un revêtement métallique mince, généralement en cuivre, accéléré et mis en forme par explosif (fig. 4).

Parmi elles, les charges creuses comportent souvent un écran inerte que contourne la détonation pour converger sur un revêtement conique d’angle réduit. La mise en vitesse du cône s’effectue de façon continûment décroissante du sommet à la base. L’implosion du métal crée un noyau massif et lent, précédé d’un jet fin et rapide qui n’emporte guère que 15 p. 100 de la matière. Du fait des conditions instationnaires de formation, la tête du jet évolue à près de 10 000 m/s et la queue à environ 2 000 m/s. Ce projectile qui s’allonge, puis se fragmente, n’est efficace qu’à courte distance.

Les charges génératrices de noyau sont munies d’une calotte sphérique métallique de faible courbure. Ce revêtement, fortement comprimé par l’attaque quasi frontale de l’onde de détonation, est légèrement plus véloce sur l’axe que sur les bords. Ces derniers convergent lentement vers l’axe pour former, avec un taux de déformation considérable, un projectile massif d’allongement proche de 3 (fig. 5). Tout le revêtement participe ici à la formation d’un noyau rapide, dont la vitesse ne dépasse guère 2 000 m/s. Une fois dans sa forme finale, ce noyau reste efficace à grande distance.

5. La métrologie en détonique

Typiquement, un kilogramme d’explosif peut libérer 6 mégajoules en 10 microsecondes. Son temps caractéristique de réaction avoisine 100 nanosecondes. L’instrumentation doit donc composer avec des phénomènes très intenses et brefs. Commandés et contrôlés électroniquement, les appareils employés (radiographiques, électroniques ou optiques) seront protégés ou consommables selon leur coût.

Les rayons X, émis pendant environ 30 nanosecondes, seront fréquemment utilisés pour visualiser la forme, la position ou l’état d’un revêtement, plus rarement d’un insert dans l’explosif. Des compteurs multichronométriques enregistrent des instants de passage d’onde ou d’impact de matière sur des capteurs. La cinématique des détonations ou des revêtements s’en déduit.

Des analyseurs numériques ou analogiques à très haute bande passante acquièrent les signaux délivrés en continu par des jauges insérées dans la matière. Un cas exemplaire est celui des jauges piézo-résistives, qui renseignent sur l’évolution des pressions dans des détonations monodimensionnelles transitoires ou permanentes, et en permettent la modélisation.

Les caméras ultrarapides ont un miroir tournant qui assure le balayage continu d’un film fixe. L’interposition d’objectifs entre miroir et film autorise une fréquence de prise de vue de plusieurs millions d’images par seconde. Dans une autre version, une fente placée en amont du miroir sélectionne selon un axe une image ultramince. Le défilement rapide de celle-ci sur le film fait de cet outil un chronomètre optique d’une résolution de quelques nanosecondes.

L’interférométrie Doppler-laser

Imaginée par M. Durand, l’interférométrie Doppler-laser met en œuvre un interféromètre de Fabry-Pérot. Dans une expérience type (fig. 6), un édifice explosif, qui comporte un générateur d’onde plane (G.O.P.) et un cylindre d’hexolite, projette un clinquant en acier. Un faisceau laser, véhiculé par une fibre optique, est rétrodiffusé par le clinquant et dirigé vers l’interféromètre avec une longueur d’onde fonction de sa vitesse.

Les cercles d’interférence sont formés sur la fente d’entrée d’une caméra, en coïncidence avec un diamètre de l’interférogramme. Le film n’est alors impressionné que par des couples de points lumineux diamétralement opposés. L’évolution temporelle des diamètres est enregistrée grâce au balayage du film, sous forme de traces symétriques. La courbe de mise en vitesse du clinquant s’en déduit aisément.

Une telle expérimentation récapitule, en les illustrant, les principaux domaines de la détonique: la génération d’un régime de détonation, ici plan, quasi permanent; le transfert d’énergie à un revêtement, avec ses composantes visibles sur la courbe de mise en vitesse (choc initial et poussée continue des produits de détonation). Elle montre en outre la précision et la fécondité des moyens de mesure modernes. Enfin, elle laisse entrevoir le potentiel de progrès que recèle la simulation numérique. La confrontation expérience-calcul est en effet une clé essentielle pour la compréhension et la modélisation des mécanismes de détonique.

détonique [ detɔnik ] n. f.

• 1973; de détoner, d'apr. l'angl. detonics

♦ Chim., phys. Science qui a pour objet l'étude des composés explosifs.

détonique [detɔnik] n. f.

ÉTYM. V. 1973; de détoner, d'après l'angl. detonics.

❖

♦ Chim., phys. Science qui a pour objet l'étude des composés explosifs. || Les recherches en détonique permettent d'améliorer les techniques d'utilisation des explosifs.

Encyclopédie Universelle. 2012.